A (Very) Brief Introduction to Game Theory
Roger Myerson, Nobel Prize winner of Economics in 2007 for his work in mechanism design theory, defines game theory as the “study of mathematical models of conflict and cooperation between intelligent rational decision-makers“.1 Of, that’s a handful! Let’s redefine this in more simple terms.
Game theory provides a mathematical framework to analyze situations in which two (or more) individuals make decisions which will affect the interests of one another.
The most famous example of a game analyzed within the framework of game theory is the prisoner’s dilemma, originally developed in 1950 by Flood and Dresher. The game itself is simple:2 two prisoners (1 and 2) are charged with a crime. They are unable to communicate with each other and are given the opportunity to A) testify that the other prisoner did the crime by himself (betrayal) or B) stay silent (cooperation).
The possible outcomes are as follows:
- if both prisoners betray each other, each gets a 2-year prison sentence
- if Prisoner 1 betrays Prisoner 2, and Prisoner 2 stays silent – Prisoner 1 is set free, Prisoner 2 spends 3 years in prison
- if Prisoner 2 betrays Prisoner 1, and Prisoner 1 stays silent – Prisoner 2 is set free, Prisoner 1 spends 3 years in prison
- if both stay silent, both prisoners will spend 1 year in prison.
Of course, the most logic course of action is for both of them to cooperate, as this will lead to a greater reward (only one year in prison). However, the dominating strategy in this case is betrayal, as it represents the best response to what the other might do.
The question now becomes – what does any of this have to do with penalties?
When Academics Meet Football
One drawback of academic experiments (and even more so for those involving game theory) is that they are usually done in a controlled laboratory setting. Conclusions are drawn assuming that the participants are doing their utmost to answer questions as truthfully as possible (it is entirely likely that participants will give answers that they think are in line with what the experimenters want, as opposed to what they actually believe). Moreover, game theory experiments in non-academic settings are incredibly sparse due to the complexity of the games involved. Here is where football penalties enter the stage.
Penalties are, by definition, “non-cooperative zero-sum games” between a penalty taker and a goalkeeper, where one side must win while the other side must lose. The so-called “strategy space” of a penalty is limited and very simple:
The goalkeeper can choose to: dive left | dive right | stay down the middle
The taker can choose to: shoot left | shoot right | shoot down the middle
What is important to note here is that the intentions of both the goalkeeper and the taker are known: the goalkeeper wants to minimize the scoring probability, while the taker wants to maximize the scoring probability (assuming of course they are not involved in match-fixing). The goalkeeper can minimize the probability by diving the same way as the kick, whereas the taker can maximize his probability by sending the goalkeeper the wrong way.
The interesting aspect in penalties is that, because the ball takes 0.4 seconds to reach the goal after it is hit by the taker with an average speed of 113 km/h,3 both the goalkeeper and the taker must move at the same time (see figure below) as the goalkeeper does not have enough time to dive after he identifies where the ball is going. The goalkeeper must make a choice before the kicker has let off any specific information as to where he will be shooting.

General Considerations for Goalkeepers
So how does a goalkeeper make his choice? In the (probably) best book written about goalkeepers – “The Outsider”4– Jonathan Wilson explores the role of goalkeepers throughout history, as well as their natural “fear of penalties”. Wilson describes that a penalty taker has a “natural side” – right-footed players (making up ~85% of the population5) strike the ball harder and more accurate with their instep, meaning that it is easier for them to shoot to their left side (vice-versa for left-footed takers). Of course, goalkeepers are aware of this, and the penalty takers are aware that the goalkeepers are aware. So, if both sides are aware, how do they go about making their decision?
As it turns out, goalkeepers have a plethora of data at their disposal with respect to a penalty taker’s past history of penalties. One famous example is Jens Lehmann’s crumpled piece of paper hidden in his sock at the World Cup quarter-final shootout vs. Argentina.

On this piece of paper were the following notes, assembled by the Germany backroom staff after they had analyzed 13,000 penalties:4
– Riquelme left
– Crespo long run-up/right short run-up/left
– Heinze left low
– Ayala 2 (my note: shirt number) waits long time, long run-up, right
– Messi left
– Aimar 16, waits long time, left
– Rodriguez 18, left
Two players on that list took penalties – Ayala and Rodriguez – and they both stuck true to the notes. Lehmann saved Ayala’s penalty, but Rodriguez’s was too accurate to save.
Now that we have established that goalkeepers have past data to back up their decision-making, as well as the knowledge of where a player is naturally inclined to shoot, what can a penalty taker do to improve his chances of scoring?
General Considerations for Penalty Takers
In 2002, economists Chiappori, Levitt and Groseclose5 analyzed 459 penalties from matches that had taken place in France and Italy over the course of three years. They developed quite a complex model and they did some advanced math to reach their conclusions, so I won’t present it here. I will instead present a summary of their findings.
When analyzing the data the authors found that if the goalie stays in the middle of the goal or chooses the wrong side relative to where the penalty is taken, a goal will be scored in 89.3% of cases if the penalty taker uses his non-natural side and in 94.4% of cases if the penalty taker shoots on his natural side (figure below).
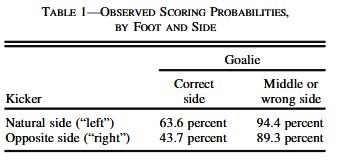
On the other hand, a goal is scored 63.6% of the time if the goalie dives the correct way and the penalty is taken on the taker’s natural side, and in only 43.7% of the time if the taker goes on his non-natural side. In addition to these data, the authors showed (figure below) that, as expected, a striker’s probability to score are similar across the three possibilities.
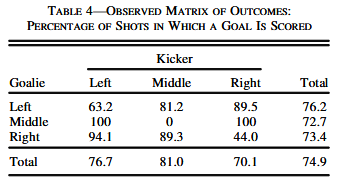
In fact, a goalie is expected to give away a goal roughly 75% of the time – this is the reason why a penalty has an xG between 0.74-0.76 (depending on model).6 Interestingly, taking a penalty down the middle of the goal results in ~81% conversion, whereas taking a penalty on your non-natural side (right -> right) results in only 70% conversion.
Concluding Thoughts and Further Reading
As shown above, taking penalties is not easy. It is a psychological battle between two actors – a goalkeeper and a penalty taker – compounded by game importance, whether the penalty is taken in a shoot-out or not, the number of fans in the stands etc. In fact, it has been shown that in a penalty shoot-out the team taking the first penalty has a 60% chance of winning, while the team going second has a consistently lower shooting percentage.7 This is likely due to psychological factors.
So, what can one do to improve their chances of scoring a penalty? They can do what Jorginho and Bruno Fernandes do – a little hop step right before shooting, which tricks the goalkeeper. The problem with this approach is that when you miss you look really dumb (like missing a Panenka). Or, they can close their eyes and blast it down the middle and hope for the best – both are valid options.
The truth is, there is no correct answer. You can try and maximize your chances by shooting on your natural side, but you risk becoming too predictable. You can choose to shoot on your non-natural side, but then you have a greater chance of missing (mostly due to the lack of accuracy resulted from lack of shooting practice to that side). What game theory tells us is that your best bet is to mix strategies and stay as unpredictable and random as possible.
As further reading I highly recommend the following:
1. “Professionals Play Minimax” – Ignacio Palacios-Huerta
2. “The Game Theory of Soccer Penalty Kicks” – William Spaniel
3. “Aim for the middle: it could be your best shot for a goal in a penalty shootout” – Stephen Woodcock
References
- Myerson, Roger B. (1991). Game Theory: Analysis of Conflict, Harvard University Press, p. 1
- Poundstone, William (1993). Prisoner’s Dilemma (1st Anchor Books ed.).
- https://www.neurotrackerx.com/post/science-penalty-kicks
- Jonathan Wilson, The Outsider: A History of the Goalkeeper, ISBN-10 :1409123197, Orion; UK ed. edition (Feb. 5 2013)
- https://pricetheory.uchicago.edu/levitt/Papers/ChiapporiGrosecloseLevitt2002.pdf
- https://fbref.com/en/expected-goals-model-explained/
- https://www.soccermetrics.net/paper-discussions/penalty-kick-shootout-paper-apesteguia-palacios-huerta
[ratemypost]
[ratemypost-result]
